今回から、数回にわたって「算数・単元別学習のコツ」をお話ししたいと思います。

初回は、「割合」です。

分数の加減乗除を学習し終えると、入試算数の最初の山場である「割合」の単元がやってきます。今後、「割合」を利用して解く問題（「相当算」、「売買損益」、「食塩水」、「比」、「速さ」、「円とおうぎ形」…）が次々と各塾のカリキュラムに配当されていきます。

と言うことは、「割合」さえ攻略してしまえば、多くの入試頻出単元に対して得意になれるチャンス到来とも考えることができますね。

ところが、この「割合」に苦戦している受験生は数多く、学習相談は後を絶ちません。

どうしてなのでしょう？

苦戦している子どもたちの様子を見てみると、「割合」に対する本質的な理解があいまい、言い換えれば、「割合のイメージ」や「割合の身体感覚」がとても希薄なように思えるのです。

その原因の一つが、教え方にあると感じています。割合の教え方は、塾によって異なるばかりか、担当の講師によってもまちまちです。その中で下の「くもわ」の図で教わった子どもたちの中に、「割合のイメージ」が育っていない子どもが多いように思います。

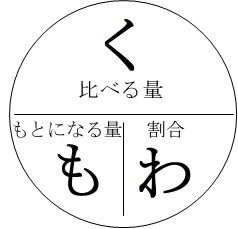
縦に並ぶと、分数の分子、分母と考えて、わり算します。　…　く÷も＝わ、く÷わ＝も

横に並ぶと、そのままかけ算します。　…　も×わ＝く

実は、そのまま、「割合の三用法（３公式）」ですね。

　（第一用法）くらべる量÷もとにする量＝割合

　（第二用法）もとにする量×割合＝くらべる量

　（第三用法）くらべる量÷割合＝もとにする量　

合理的で素晴らしい「魔法の道具」のように見えますが、ここに落とし穴があります。

理解が進まないうちに、「くもわ」の図にあてはめて解くことで、基本問題はとりあえず正解できます。でも、少しでも問われ方が変化したり、わずかでも複雑になると、とたんに鉛筆が止まります。

それは、「割合の身体感覚」が育っていないからです。

割合はあらゆる単元に応用される重要な概念ですから、頭の中だけで分かっているだけでは使いこなせないのですね。

そこでここから、割合を正しく学習する方法をご説明していきたいと思います。

「分かる」から「できる」へとステップアップさせていきましょう。